Common Point
When all functions of a family of curves go through a common point, a bundle of functions occurs.
!
Remember
Not every family of curves has a common point.
i
Hint
If there is a common intersection of all of the families function graphs, then there must be a location $x$ where the additional parameter disappears.
The intersection is therefore at this x-value.
The intersection is therefore at this x-value.
Example
$f_a(x)=x^2+ax$ (with $a\in\mathbb{R}$)
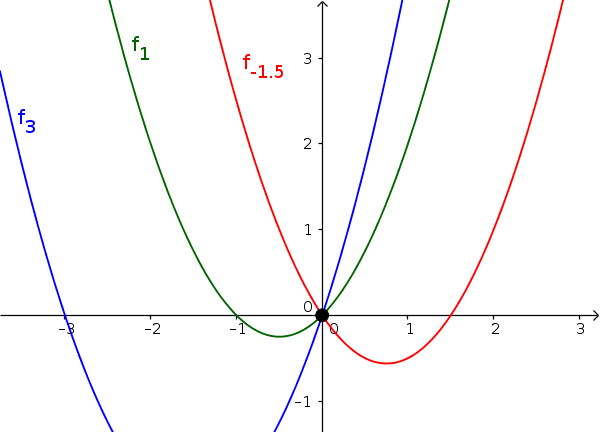
- $\color{blue}{f_3(x)=x^2+3x}$
- $\color{green}{f_1(x)=x^2+x}$
- $\color{red}{f_{-1.5}(x)=x^2-1.5x}$
