Volumen
Das Volumen (Formelzeichen: $V$) bezeichnet das Fassungsvermögen eines Körpers.
Die Einheit wird in Kubik (z.B. $m^{ 3 }$) angegeben.
Umrechnung
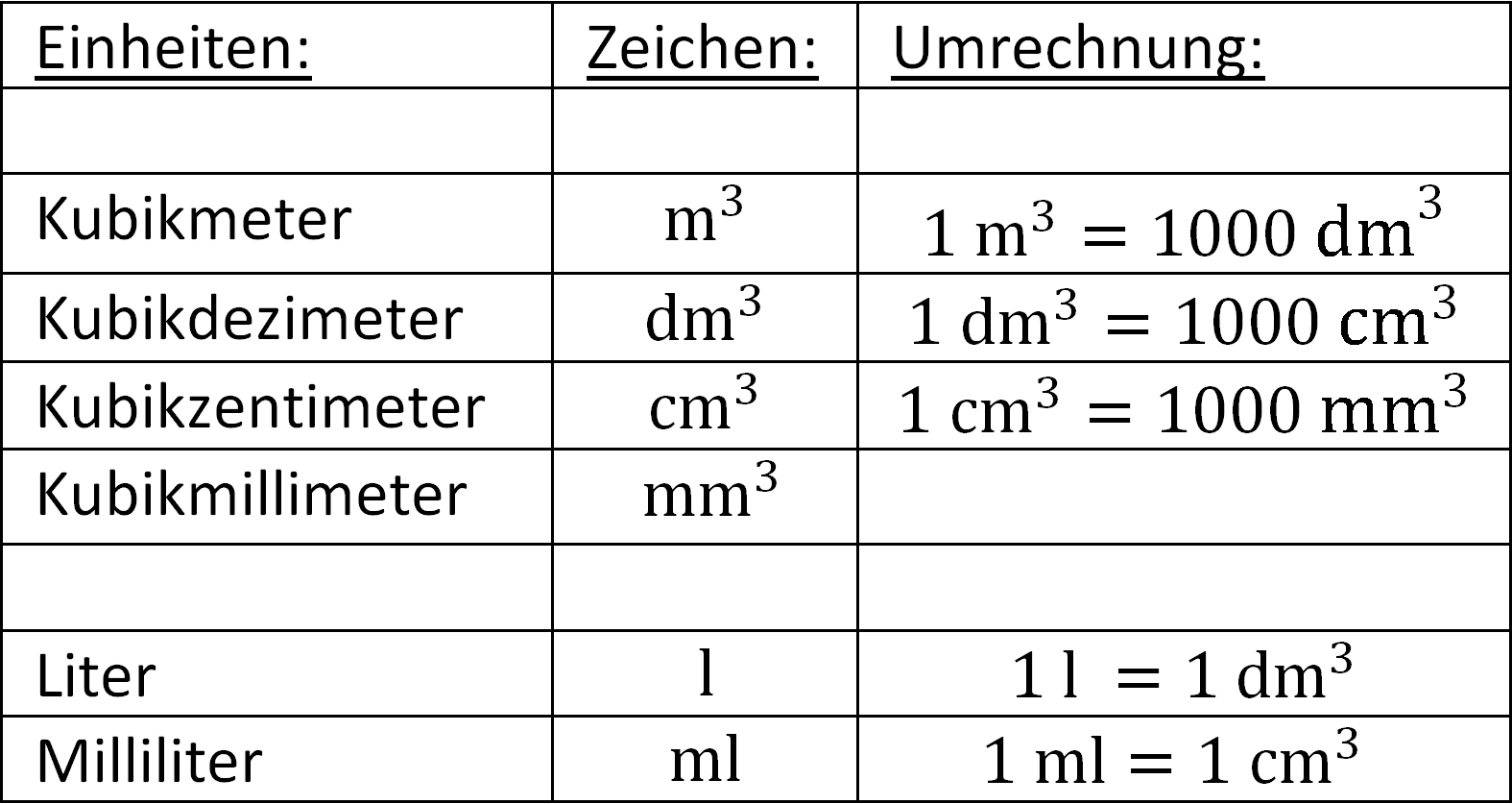
!
Beachte
Die Umrechnung von Volumeneinheiten erfolgt mit dem Faktor 1000 statt den üblichen 10, denn:
$1m=10dm=100cm$
Also gilt für Volumeneinheiten entsprechend:
$(1m)^3=(10dm)^3=1000dm^3$ $=1\,000\,000cm^3$Wichtige Formeln
1) Würfel:

$V=\color{red}{a}\cdot\color{red}{a}\cdot\color{red}{a}$
$A_O=6\color{red}{a}^2$

$V=\color{red}{a}\cdot\color{red}{a}\cdot\color{red}{a}$
$A_O=6\color{red}{a}^2$
2) Quader:

$V=\color{red}{a}\cdot \color{blue}{b}\cdot \color{green}{c}$
$A_O=2(\color{red}{a}\color{blue}{b} + \color{red}{a}\color{green}{c} + \color{blue}{b}\color{green}{c})$
3) Pyramide:
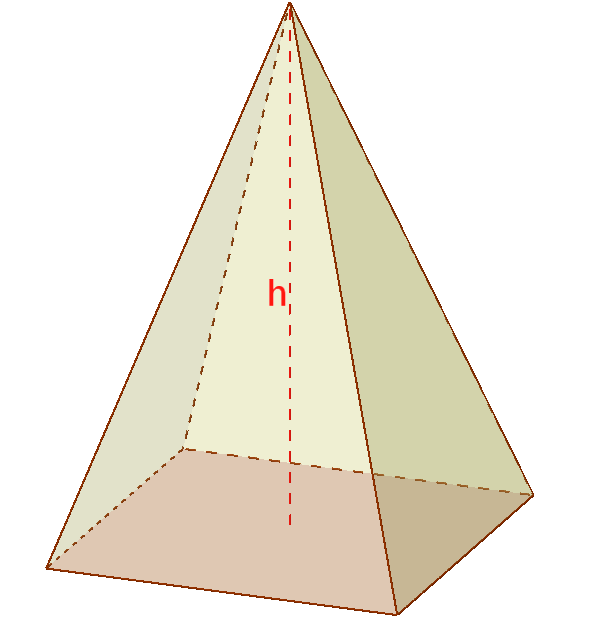
$V=\frac{ 1 }{ 3 } \cdot A_{G}\cdot \color{red}{h}$
$A_O=A_G+A_M$

$V=\frac{ 1 }{ 3 } \cdot A_{G}\cdot \color{red}{h}$
$A_O=A_G+A_M$
i
Info
$A_G$ - Flächeninhalt der Grundfläche („Boden“)
$A_M$ - Mantelfläche (Summe aus den Flächeninhalten der Dreicke)
$A_M$ - Mantelfläche (Summe aus den Flächeninhalten der Dreicke)
4) Zylinder:

$V=\pi\cdot \color{red}{r}^2\cdot\color{green}{h}$
$A_O=2\pi\color{red}{r}(\color{red}{r}+\color{green}{h})$

$V=\pi\cdot \color{red}{r}^2\cdot\color{green}{h}$
$A_O=2\pi\color{red}{r}(\color{red}{r}+\color{green}{h})$
5) Kugel:
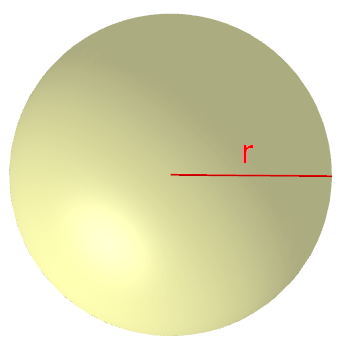
$V=\frac{4}{3}\cdot\pi\cdot\color{red}{r}^{ 3 }$
$A_O=4\pi\color{red}{r}^2$

$V=\frac{4}{3}\cdot\pi\cdot\color{red}{r}^{ 3 }$
$A_O=4\pi\color{red}{r}^2$
6) Kegel:
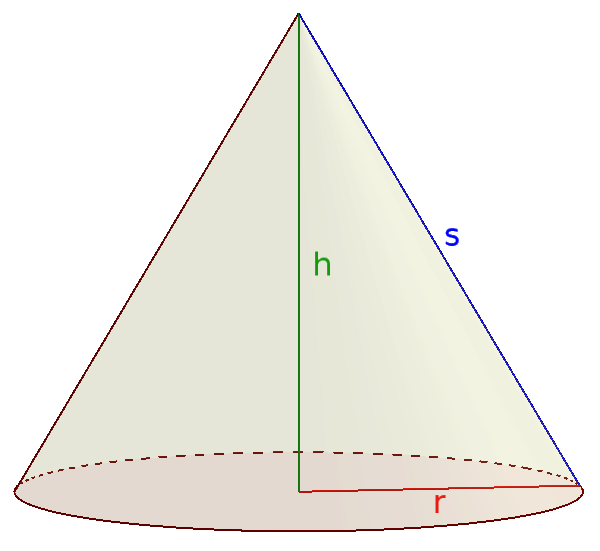
$V=\frac{1}{3}\cdot\pi\cdot\color{red}{r}^{ 2 }\cdot\color{green}{h}$
$A_O=\pi\color{red}{r}(\color{red}{r}+\color{blue}{s})$

$V=\frac{1}{3}\cdot\pi\cdot\color{red}{r}^{ 2 }\cdot\color{green}{h}$
$A_O=\pi\color{red}{r}(\color{red}{r}+\color{blue}{s})$
