Mathe ↠ Quadratische Funktionen ↠ Die Normalparabel

Die Normalparabel

Die Normalparabel ist der Graph der einfachsten quadratischen Funktion. Sie besitzt die Funktionsgleichung $y=x^2$

i

Eigenschaften

  • Graph symmetrisch zur y-Achse
  • Koordinatenursprung ($0|0$) ist Scheitelpunkt und tiefster Punkt des Graphen
  • Graph fällt im 2. Quadranten und steigt im 1. Quadranten

Beispiel

Zeichne die Normalparabel.

  1. Wertetabelle anlegen

    Die Normalparabel besitzt die Funktionsgleichung $f(x)=x^2$. Für $x$ setzen wir jetzt Werte von -3 bis 3 ein.

    $f(-3)=(-3)^2=9$
    $f(-2,5)=(-2,5)^2=6,25$
    $f(-2)=(-2)^2=4$
    ...
    $f(3)=3^2=9$

  2. Werte in ein Koordinatensystem eintragen


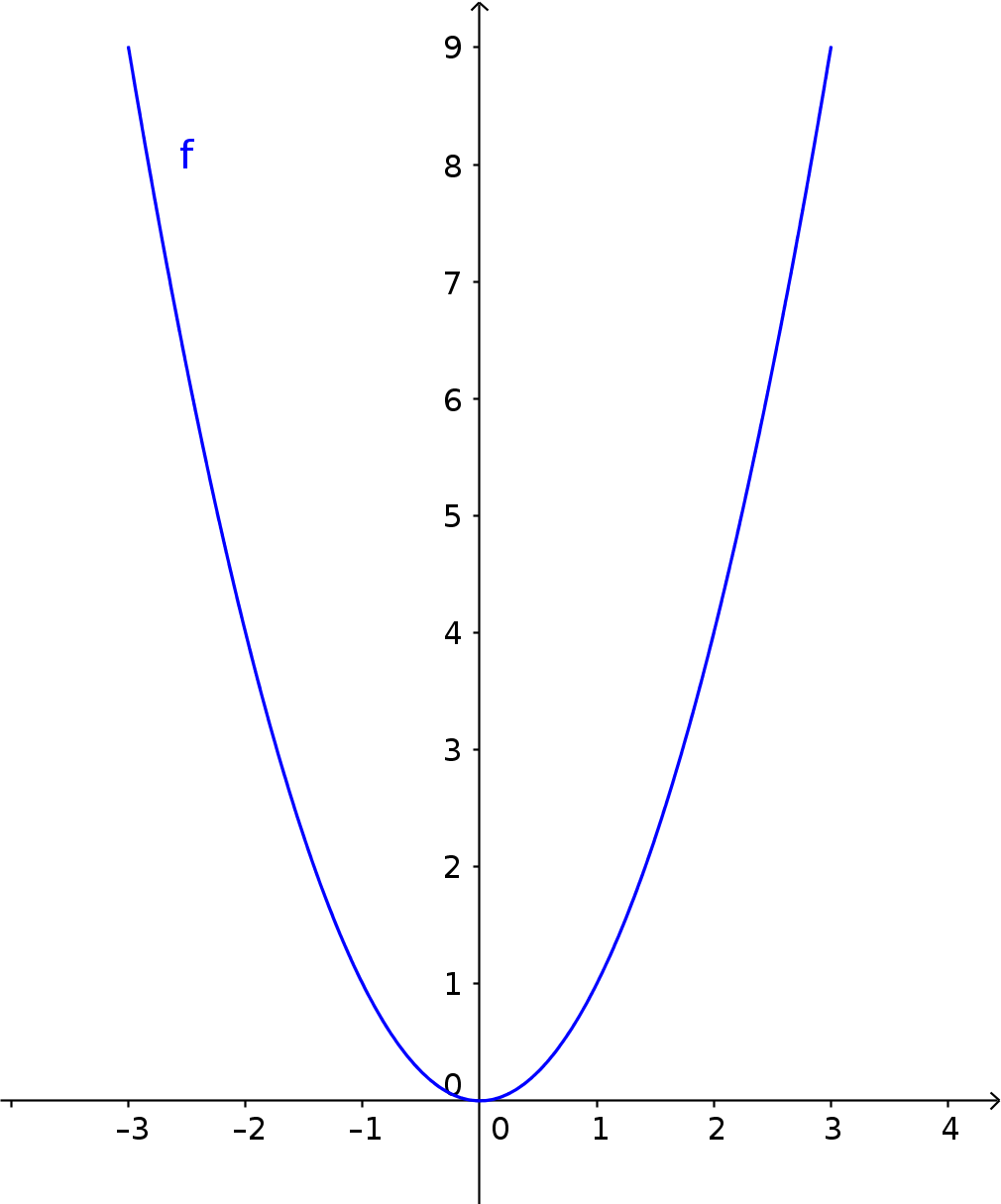
    Normalparabel

Einstieg Parabeln: Einleitung, Normalparabel, Formen, Quadratische Funktion , Quadratische Gleichung

Kooperation mit dem Kanal von Mister Mathe

Mit dem Abspielen dieses Videos akzeptierst du YouTubes Datenschutzerklärung.

Videos von YouTube immer laden

Eine quadratische Funktion ist eine Funktion zweiten Grades, d. h. $x^2$ ist die größte Potenz, mit der allgemeinen Form

$f(x)=ax^2+bx+c$

Durch quadratische Ergänzung lässt sich diese auch in die Scheitelpunktform umwandeln. Hier können der Streckfaktor $a$ sowie die Koordinaten des Scheitelpunktes $S(\color{blue}{d}|\color{green}{c})$ direkt abgelesen werden.

$f(x)=a(x-\color{blue}{d})^2+\color{green}{c}$

Die Normalparabel mit der Funktionsgleichung $f(x)=x^2$ ist deshalb eine

  • nicht verschobene
  • nicht gestreckte
  • nach oben geöffnete

Parabel mit dem Scheitelpunkt $S(0|0)$. Der Graph einer quadratischen Funktion ist immer symmetrisch zur Geraden, die durch den Scheitelpunkt verläuft. Die Normalparabel ist deshalb symmetrisch zur y-Achse.