Die stehenden Wellen
Die Überlagerung zweier entgegengesetzt ausbreitender Wellen gleicher Frequenz und gleicher Amplitude kann als stehende Welle aufgefasst werden.
Reflexion von Wellen
Dieses Phänomen tritt z. B. auf, wenn Wellen an Objekten reflektiert werden.
Diese Welle läuft nämlich in sich selbst zurück und interferiert dann mit sich selbst.
Es bilden sich Punkte, an denen sich die Wellen zu jeder Zeit auslöschen (Knoten) und Stellen, wo sich die Wellen addieren (Bäuche).
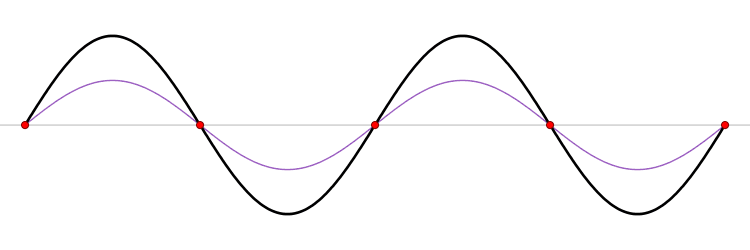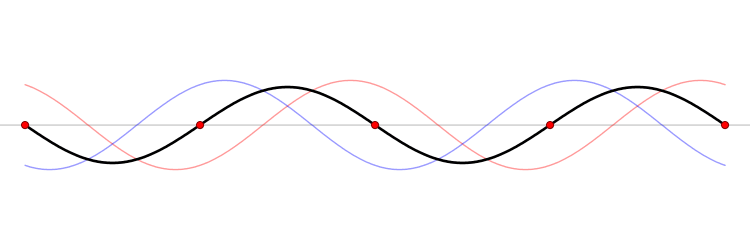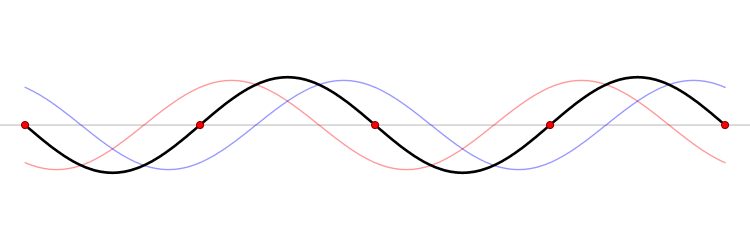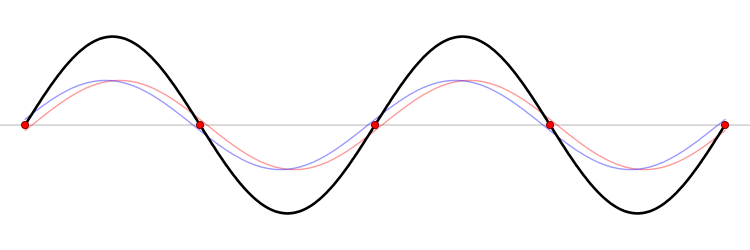
Zum Bild: Beispiel einer stehenden Welle (schwarz) und der Knotenpunkte (rot)
Tipp
Bedingung für die Entstehung stehender Wellen
Die Bedingung dafür, ob eine stehende Welle entsteht, hängt von der Länge $L$ des schwingenden Körpers und den Enden ab.
Merke
Offene Enden bedeutet, dass kein Phasensprung bei der Reflexion auftritt
Festes Ende bedeutet, dass ein Phasensprung von $\pi$ auftritt.
Zwei gleiche Enden
Bei zwei gleichen Enden entsteht an beiden Enden ein Phasensprung und deshalb Knoten.
Die Bedingung ist:
$n = 0,1,2,3,...$
Ein offenes und ein festes Ende
$n = 0,1,2,3,...$
Schwingungen
Bei $n=1$ nennt man es Grundschwingung. Danach die n. Oberschwingung.

