Fläche zwischen Funktionsgraphen
Mithilfe des bestimmten Integrals lässt sich auch die Fläche zwischen zwei Funktionsgraphen berechnen.

Gesucht ist der eingeschlossene Flächeninhalt von zwei Funktionen im Intervall $[a;b]$. Dazu subtrahiert man die kleinere von der größeren Fläche ($f(x) > g(x)$ im Intervall $[a;b]$):
$A=\int_a^b f(x)\,\mathrm{d}x\,-$ $\int_a^b g(x)\,\mathrm{d}x$
Jetzt kann noch die Summenregel rückwärts angewendet werden.
Damit die Formel auch gilt, wenn $f(x) < g(x)$ im Intervall $[a;b]$, setzt man noch Betragsstriche.
$A=|\int_a^b (f(x)-g(x))\,\mathrm{d}x|$
i
Tipp
Die Formel ist unabhängig von der Lage der Fläche bezüglich der x-Achse. Es ist also nicht wichtig, ob sich die Fläche über oder unter der x-Achse befindet.
i
Vorgehensweise
- Differenzenfunktion bilden
- Bestimmtes Integral aufstellen und berechnen
- Flächeninhalt bestimmen
Beispiel
Berechne den Flächeninhalt zwischen den Graphen der Funktionen $f(x)=\frac12x^2+1$ und $g(x)=-\frac12x^2+x$ über dem Intervall $[0,5; 2]$
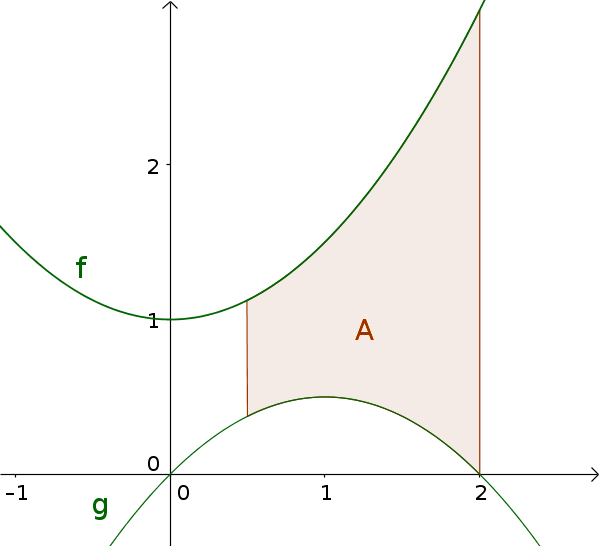
-
Differenzenfunktion
Zuerst wird $g(x)$ von $f(x)$ subtrahiert und zusammengefasst.
$f(x)=\frac12x^2+1$
$g(x)=-\frac12x^2+x$
$h(x)=f(x)-g(x)$ $=(\frac12x^2+1)-$ $(-\frac12x^2+x)$ $=x^2-x+1$ -
Bestimmtes Integral aufstellen
Integrationsgrenzen und $h(x)$ in das bestimmte Integral einsetzen und Integral berechnen.
$\int_a^b (f(x)-g(x))\,\mathrm{d}x$ $=\int_a^b h(x)\,\mathrm{d}x$
$\int_{0,5}^2 (x^2-x+1)\,\mathrm{d}x$ -
Integral berechnen
$\int_a^b h(x) \, \mathrm{d}x$ $= [H(x) + C]_a^b$ $= H(b) - H(a)$
$H(x)=\frac13x^3-\frac12x^2+x$
$\int_{0,5}^2 (x^2-x+1)\,\mathrm{d}x$ $=[\frac13x^3-\frac12x^2+x]_{0,5}^2$ $=(\frac13\cdot2^3-\frac12\cdot2^2+2)-$ $(\frac13\cdot0,5^3-\frac12\cdot0,5^2+0,5)$
$=\frac83-\frac{5}{12}$ $=\frac94$ -
Flächeninhalt bestimmen
$A=\int_{0,5}^2 (x^2-x+1)\,\mathrm{d}x$ $=\frac94$ $=2,25$
Fläche zwischen zwei Graphen ohne Schnittpunkt, Fläche zwischen zwei Kurven mit Integral berechnen
Kooperation mit dem Kanal von Mister Mathe

