Natürliche Logarithmusfunktion

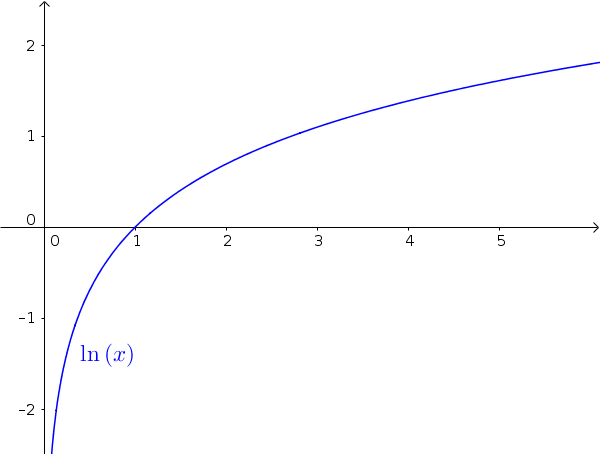
Die Umkehrfunktion der e-Funktion ist die natürliche Logarithmusfunktion oder ln-Funktion:

$f(x)=\ln(x)$

Merke

Die ln-Funktion ist eine Logarithmusfunktion mit der eulerschen Zahl als Basis:

$\ln(x)=\log_e(x)$

Tipp

Der logarithmus naturalis kurz $\ln$ ist ein Logarithmus mit der Basis $e$:
$\ln=\log_e$

Merke

Da die natürliche Logarithmusfunktion die Umkehrfunktion der e-Funktion ist, gilt folgendes Rechengesetz:

$x=\ln(e^x)$ $=e^{\ln(x)}$

Tipp: Die Regel ist bei der Herleitung der Ableitung allgemeiner Exponentialfunktionen von Vorteil.