Функция натурального логарифма

Обратная функция от естественной показательной функции, это функция натурального логарифма или ln-функция:

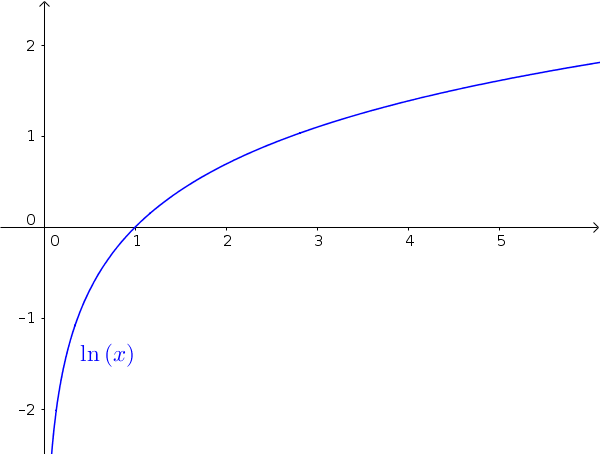
$f(x)=\ln(x)$

Запомните

Функция натурального логарифма- это логарифмическая функция с числом Эйлера в качестве основы:

$\ln(x)=\log_e(x)$

Подсказка

Натуральный логарифм, коротко $\ln$, является логарифмом с основанием $e$:
$\ln=\log_e$

Запомни

Поскольку натуральная логарифмическая функция является обратной функцией экспоненциальной функции с основанием e, то применяется следующий закон вычисления:

$x=\ln(e^x)$ $=e^{\ln(x)}$

Совет: это правило полезно при выводе производной от общих экспоненциальных функций.