Calculating areas by partitioning the interval

An exception to calculating areas are functions with sign changes in the interval $[a; b]$. This means that the area is partly above and partly below the x-axis.

Example

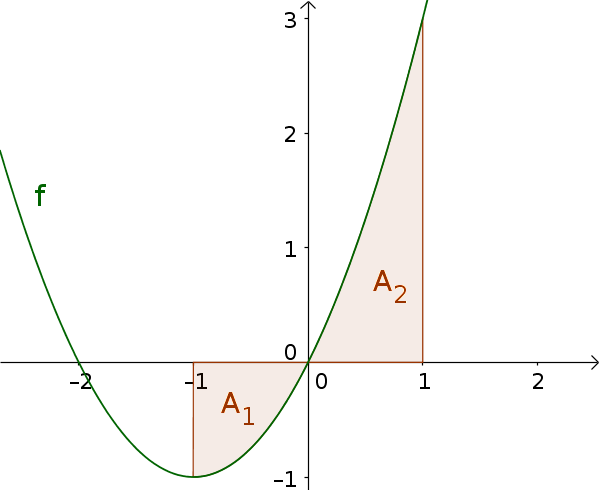
Calculate the area between the graph of the function $f(x)=x^2+2x$ and the x-axis over the interval $[-1; 1]$

1. Find intervals

   First, calculate the zero(s) of the function.
   $x^2+2x=0$
   (Solve quadratic equation, e.g. remove brackets)
   $x(x+2)=0$
   $x_{N_1}=0$ and $x_{N_2}=-2$
   
   $x_{N_1}=0$ is in the interval $[-1; 1]$. Therefore, the area must be divided into two parts:
   $A_1$ over $[-1;0]$
   $A_2$ over $[0;1]$
   

2. Find and calculate definite integrals

   For both intervals, an integral must now be calculated.
   $\int_a^b f(x) \, \mathrm{d}x$ $= [F(x) + C]_a^b$ $= F(b) - F(a)$
   $F(x)=\frac13x^3+x^2$
   
   $A_1$ over $[-1;0]$:
   $\int_{-1}^0 (x^2+2x) \, \mathrm{d}x$ $= [\frac13x^3+x^2]_{-1}^0$ $= \frac13\cdot0^3+0^2 -$ $\frac13\cdot(-1)^3+(-1)^2$
   $=0-\frac23$ $=-\frac23$
   
   
   $A_2$ over $[0;1]$:
   $\int_0^1 (x^2+2x) \, \mathrm{d}x$ $= [\frac13x^3+x^2]_0^1$ $= \frac13\cdot1^3+1^2 -$ $\frac13\cdot0^3+0^2$
   $=\frac43-0$ $=\frac43$
   

3. Determine area

   Now the area of each partition has to be determined and then added.
   $A_1=|\int_{-1}^0 f(x)\,\mathrm{d}x|$ $=|-\frac23|$ $=\frac23$
   $A_2=\int_0^1 f(x)\,\mathrm{d}x$ $=\frac43$
   
   $A=A_1+A_2$ $=\frac23+\frac43=2$